Let’s start with this problem that appeared on my news feed.

WARNING: Stop reading if you want to solve it yourself first.
Recall from high school maths that angle subtended by an arc (or chord) to a point on the circumference of the circle does not change as the point moves around the circle.
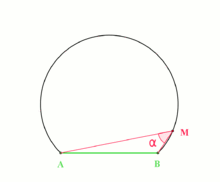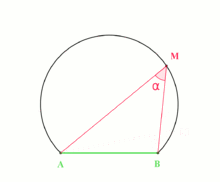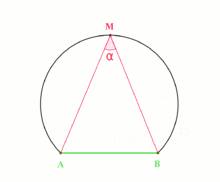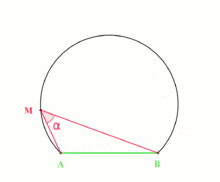
We can use this to transform the given angle problem into one that deals with lengths. For the rest of this post, AB is taken to mean the minor arc on the circle between points A and B, and ABC is taken to mean \angle ABC.

Here, I’ve colour coded the given conditions into the image to make it easier to visualize the argument below.
- Red: If the angles are the same, then the arc length must be the same. So AB = CD
- Blue: What follows is thus AC = BD because they share CB.
- Green: BX corresponds to angle 40°.
- Purple: DX corresponds to angle 35°.
From the diagram, we can see that the blue segment = green segment - purple segment, and corresponds to 40° - 35° = 5°.
Did I sense doubt from you? Did you say “we are dealing with angles after all, does it really work if we translate them into arc lengths?”?
Let’s map each step back into a problem that deals with angle.
- Blue: DXB is also x° degrees because they share the angle CXB.
- DXB = DCB, and XCB = XAB because they are subtended by the same chord.
- x° = DCB = XCB - XCD = 40° - .5°.
If you are observant, you might notice that we did not use the given value 75 in the original question. Indeed, I suspect that was a red herring so that people do not immediately guess the answer to be the difference between the larger number and the smaller number.
An interesting takeaway concept from this is that sometimes we can transform a problem from one domain into another, solve it in the other domain, and then transform the solution back to the original domain. This is also a key idea in homomorphism, but more on that some other time.