I’ve been playing Euclidia and I love it so far. Here’s some of the interesting challenges that I was stuck at for a while. The stage which the puzzle happens is included in the brackets.
The following challenges must be solved using only elementary Euclidean operations, which is defined as a construction that can be made with a real compass and straight edge. Marking intersections are not counted as an operation. This rules out the use of protractors to measure angles.
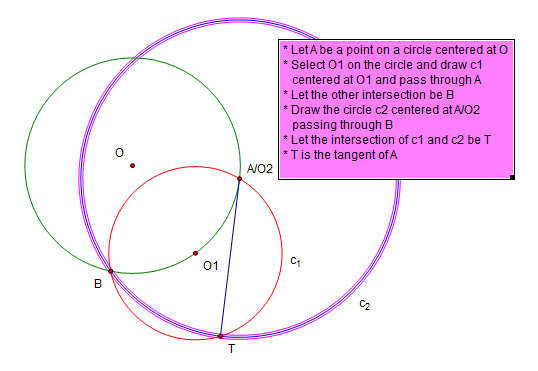
Constructing tangent to circle at a point (2.8)
Given a circle and a point, construct the tangent to the circle at that point with 3 elementary operations.
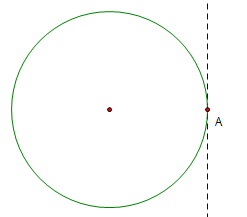
Erecting a perpendicular on a line (2.7)
Given a line and a point on the line, construct a perpendicular at that point with 3 elementary operations.
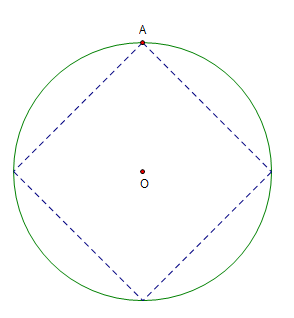
Inscribing a square (1.7)
Given a circle and a point on the circle, construct the inscribed circle with 7 elementary operations. The 4 lines are part of the operations!
Solution
Constructing a tangent
This works by proving that TAO1 is the same angle as ABO1. By draing a circle centered at O, we reflected B against line AO1 to T.
Erecting a perpendicular
This uses the fact that BC is the diameter so A is right angle.
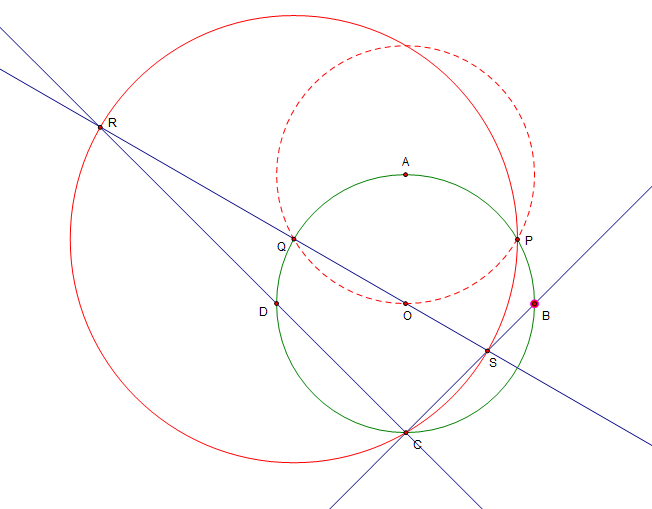
Inscribed circle
This feels almost like magic to me.
We first draw two auxillary circles, label the intersections and construct R as follows: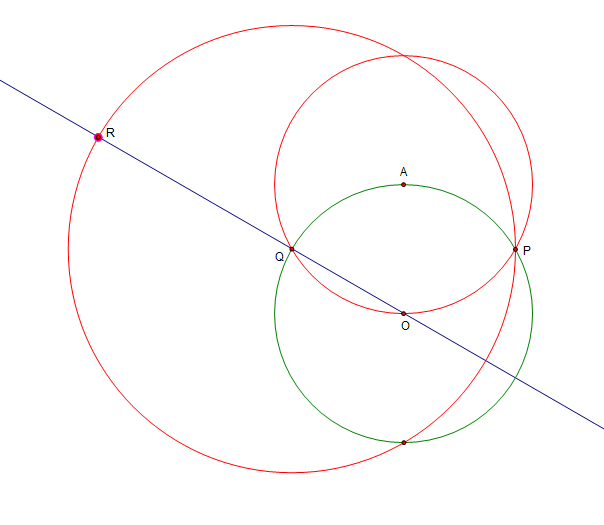
Let R intersect the original circle at C. This is the bottom of the square. Let the line RC intersect the original circle at D, This is one of the points of the square too.
Next comes the crux, label the intersection of the line OQ and the circle centered at Q, call it S. This is the diameter and hence SCR is a right angle! Extending that line to intersect the original circle will give us B, the last point of the square.